P2 - Predicting forces and shapes for invasion of apicomplexan parasites into host cells
Predicting forces and shapes for invasion of apicomplexan parasites into host cells
Invasion into host cells is a vital step in the life cycle of apicomplexan parasites. Therefore, understanding the invasion mechanism is key for identifying potential therapeutic measures to prevent the disease. Advances in microscopy have led to a significant increase of our knowledge on the parasite architecture in the past years: microtubules that extend from the apical end throughout a large part of the parasite, an actin network at the dorsal end, and a perforated inner membrane complex that spreads along the microtubules. The architecture hints several invasion mechanisms that include the classical linear-motor model and the push-and-pull model. Recent experiments also hint important roles of the lipid-bilayer membranes; in particular, parasites have been observed to invade into giant unilamellar vesicles. State-of-the-art theory and computer simulations will allow us to test hypotheses for the invasion mechanism based on optical microscopy images and to quantitatively predict the involved forces. For Toxoplasma, we aim to address the following questions: What can we learn from parasite shape about its cytoskeletal architecture? Can discrete bond-adhesion explain the apical end of the banana-shaped parasite get into contact with the host plasma membrane? What is the role of parasite deformability for adhesion and invasion? Which passive and active forces and parasite shapes occur while the parasite squeezes through the tight junction? How does the tight junction hinder invasion of the entire parasite and in particular the stiff nucleus of the parasite? What is a minimum size of a pore that a parasite can actively squeeze through? What is the time for complete invasion? What is the role of reorganisation of the cytoskeleton, linear-motor forces at the tight junction, and contractile actin forces within the push-and-pull model for invasion of wild-type and genetically modified parasites? In particular, we will stdy: (a) Forces on microtubules, actin network, and plasma membrane for maintaining the non-spherical shape of free parasites. (b) Formation of discrete bonds in early stages of parasite adhesion to the host and resulting parasite and host deformation. (c) Forces and parasite shape deformations that occur while the parasite squeezes through a circular pore. (d) Forces and parasite shapes upon interaction with giant unilamellar vesicles.
Apicomplexans - abundant and versatile parasites
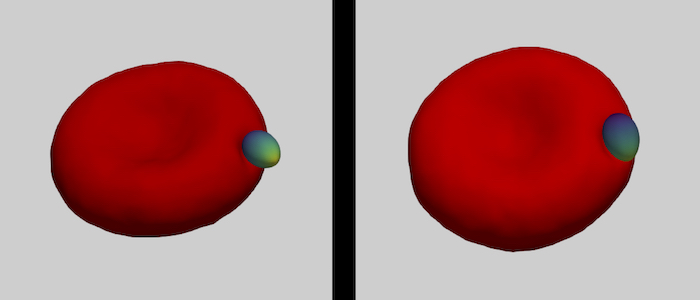
The family of apicomplexa contains a huge variety of parasites, among them Plasmodium (malaria) and Toxoplasma (toxoplasmosis). Apicomplexan parasites cause various diseases— different members invade different host cells—, and range in size from one micrometre for Plasmodium to ten micrometres for Toxoplasma. Apicomplexan parasites have a common cytoskeletal architecture and a highly polarised organisation with a well-defined apical pole, leading to an egg-like (Plasmodium merozoites) or banana-like (Toxoplasma tachyzoites) shape. When in touch with the host plasma membrane, the parasites reorient to invade with the pointed, apical end first. For the entry of Plasmodium into red blood cells, it has been demonstrated on the basis of computer simulations for stiff, egg-shaped parasites that host deformability plays a crucial role for parasite alignment prior to entry; a passive role and the elasticity of the red blood cell for parasite reorientation is also supported by recent studies on the importance of calcium signalling in the host for pre-invasion. Interestingly, host membrane tension and the erythrocyte cytoskeleton have been shown experimentally to crucially affect invasion for both, Plasmodium, and of Toxoplasma.
Modelling fluid and polymerised membranes

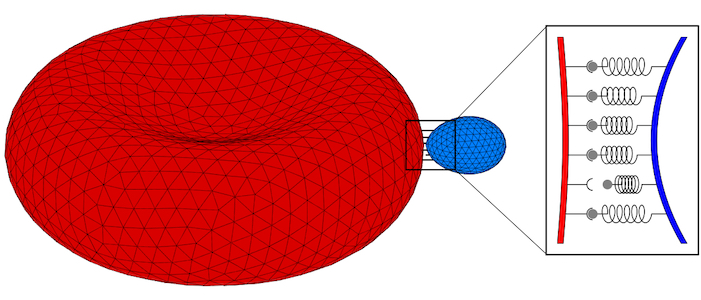
Fluid (e.g. lipid bilayer membranes) and polymerised membranes (e.g. a cortical cytoskeleton) can be modelled using a continuum model for various model systems. For fluid membranes, such as lipid bilayers, the curvature-elastic properties originate from the self-assembled lipid architecture of a fluid lipid bilayer, where hydrophilic head groups are facing the water and the hydrophobic tails forming the core of the bilayer. For initially planar lipid bilayers, deformation energy costs that result from a compression of the ‘inner’ monolayer and a stretching of the ‘outer’ monolayer are locally proportional to the squared mean curvature of the membrane with the bending modulus determining the proportionality factor. On the scale of a cell (a parasite, a giant vesicle) the actual thickness of the lipid bilayer membrane can be neglected. This results in the Helfrich Hamiltonian, where a lipid bilayer is represented by a mathematical surface, whose deformation energy is characterized by a bending rigidity and a preferred, spontaneous curvature. For computer simulations and numerical calculations, we discretize the Helfrich Hamiltonian for fluid membranes on triangulated surfaces. Edges may be considered as harmonic springs for membranes that are also subject to a shear modulus. In computer simulations, triangulated surfaces can adopt to arbitrary shapes and yet allow us to calculate deformation energies with very high accuracy.
Receptor-mediated adhesion
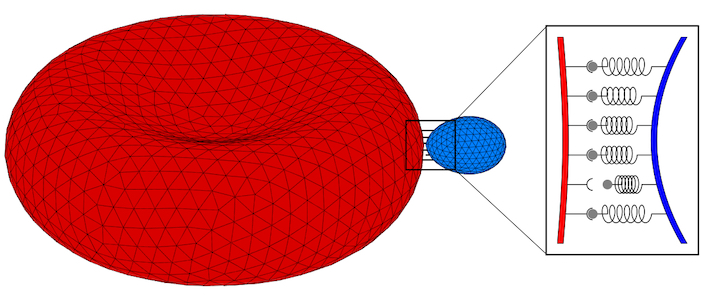
Parasites adhere to hosts using discrete bonds between the parasite and the host plasma membrane—a process that is also key for adhesion of infected cells to the endothelium. In both cases, bonds will form and break dynamically between the vertices of the triangulated surfaces that represent the membranes. The resulting adhesion bond dynamics will allow us to predict wrapping states along with parasite and host deformations. We will initially use the kinetic bond parameters obtained in our previous work on the adhesion of Plasmodium to red blood cells for Toxoplasma at various model host systems—and vary the parameters around these initial values. We will aim to calibrate our kinetic bond parameters by matching parasite displacement on host plasma membranes with experimental data for Toxoplasma.
Accurate predictions of parasite invasion states
Various models have been hypothesized for the invasion mechanism of apicomplexa, which traditionally focus on parasite activity but may also involve host contributions. Assuming an egg-shaped, rigid parasite, a motor complex generates force between the inner membrane complex of the parasite and the host. For this model system, numerical calculations can predict invasion states for various combinations of a parasite-host adhesion strength, tension of the host plasma membrane, and line tensions at the tight junction. For low adhesion strengths free parasites are predicted, for medium adhesion strengths and high membrane tensions partial-wrapped states are predicted where the parasite is stuck at the host membrane, and for high adhesion strengths fully invaded parasites are predicted. Active biological processes can be interpreted based on the wrapping predictions. Transitions between the states are often related with an energy barrier, and can be overcome by lipids shed by the parasite into the host plasma membrane, spontaneous curvature induced by the parasite in the host plasma membrane, as well as a motor complex that generates a driving force at the tight junction. Within the linear motor model for Plasmodium, molecular motors act on the parasite at the tight junction where it squeezes itself through the plasma membrane inside a vacuole. Within the push-and-pull model for Toxoplasma, the parasite’s nucleus is “pushed” through the tight junction into the host cell by contraction of the actin network at the back and “pulled” through the tight junction by microtubules.