1. Basics – Nlevel-Systeme, quantenmechanische Oszillatoren und Kopplungen
Um zu beginnen, erstellen wir eine Simulation für das Beispiel von der Startseite: zwei Qbits, die über eine Mode des Lichtfelds gekoppelt sind.
Die drei zentralen Entitäten der Toolbox sind die Klassen System, Nlevel und Qoscillator.
Die System-Klasse ist eine Containerklasse, die alle Elemente einer Simulation enthält. Jeder Teil des QDT-Codes beginnt mit der Deklaration eines System-Objekts, das anschließend mit allen Elementen gefüllt wird, die Teil der Simulation sind.
Ein Nlevel-Objekt stellt ein Quantensystem dar, das – wie der Name schon sagt – n diskrete Energieniveaus hat. Die Energielücken zwischen diesen Niveaus sind Parameter eines Nlevel-Objekts.
Ein Qoscillator-Objekt stellt einen quantenmechanischen harmonischen Oszillator dar und kann zur Modellierung verschiedener bosonischer Anregungen verwendet werden, beispielsweise einer Mode des Lichtfelds oder eines Plasmons in einer Kavität.
Nlevel- und Qoscillator-Objekte werden oft als Subsysteme bezeichnet.
Wie sieht das in der Praxis für unser Beispiel aus? Hier ist der Code, der ein System aus zwei Qbits implementiert, die über eine Lichtfeldmode gekoppelt sind.
1 | s = System; % create a System object |
Gehen wir das Zeile für Zeile durch. In Zeile 1 wird ein System mit dem Namen s erstellt. Wir nennen es s, weil das zu kurz ist und wir viele Male Funktionen aus der Systemklasse aufrufen müssen. Als nächstes wird in Zeile 2 die addentity-Funktion der Systemklasse aufgerufen, um der Simulation ein Subsystem hinzuzufügen. Diese Methode nimmt zwei Parameter an, das Subsystem, das dem Systemobjekt hinzugefügt werden soll, und einen Namen, mit dem wir dieses Subsystem fortan ansprechen können. Die Nlevel-Klasse nimmt einen Zeilenvektor an, der die Energieunterschiede zwischen allen Niveaus des Subsystems enthält. Eine [1] entspricht dabei einer einzelnen Energielücke von 1 a.u. (QDT läuft vollständig mit atomaren Einheiten) und damit einem Zwei-Niveau-System – einem Qbit. Wenn wir ein Drei-Niveau-System erstellen wollten, würden wir einen Drei-Level-Vektor wie [1 2] übergeben. Die Energie zwischen dem Grundzustand und dem ersten angeregten Zustand wäre 1 a.u., die Lücke zwischen dem ersten und zweiten angeregten Zustand 2 a.u.. Beachten Sie, dass eine Energielücke von 1 a.u. einem Übergang im extremen UV-Bereich entsprechen würde, der für die meisten Experimente ziemlich unrealistisch ist und hier nur der Einfachheit halber verwendet wird.
Jeder Funktions- und Klassenkonstruktor in QDT wird von einer Matlab-Dokumentation begleitet, die Beispiele und vollständige Informationen zur möglichen Syntax enthält.
Zeile 3 ist Zeile 2 sehr ähnlich. Ein quantenmechanischer harmonischer Oszillator wird der Simulation hinzugefügt. Die Klasse Qoscillator nimmt zwei Parameter: die Anzahl der simulierten Niveaus (diese sollte so gewählt werden, dass das höchste Niveau zu jeder Zeit eine geringe Besetzung aufweist; ein echter quantenmechanischer harmonischer Oszillator hat eine unendliche Anzahl von Niveaus) und die Energielücke zwischen diesen Niveaus (die ein Skalar sein muss, da alle Energieniveaus gleich weit voneinander entfernt sind). Wieder wird ein Wert von 1 a.u. gewählt, damit die Subsysteme resonant sind.
In Zeile 4 wird der Simulation ein zweites Qbit hinzugefügt.
Jetzt fehlen nur noch die Dipol-Dipol-Kopplungsterme. Um diese hinzuzufügen, stellt die Systemklasse eine addCoupling-Methode bereit, die die Namen der zu koppelnden Subsysteme und die Kopplungsstärke als Parameter annimmt.
Und jetzt sind wir fertig. Sechs Codezeilen (fünf, wenn Sie die erste nicht mitzählen) sind alles, was benötigt wird. Jedes Element der Stift- und Papierversion entspricht einer Codezeile. Um die Simulation auszuführen, müssen wir lediglich einen Zeitschritt und eine maximale Simulationszeit festlegen und den Simulationsbefehl der Systemklasse ausführen. Die Dichtematrix für jeden Zeitschritt wird berechnet und in einer Variablen namens rho_hist im Systemklassenobjekt s gespeichert. Hier ist der vollständige Code:
1 | clear; close all; |
setState versetzt qbit1 zu Beginn der Simulation in einen angeregten Zustand. Andernfalls würden alle Subsysteme im Grundzustand starten und da wir der Simulation keinen externen Laserpuls hinzugefügt haben, würde nichts passieren. Die System-Klasse bietet eine Reihe von Funktionen zur Analyse der Ergebnisse einer Simulation. Der Code
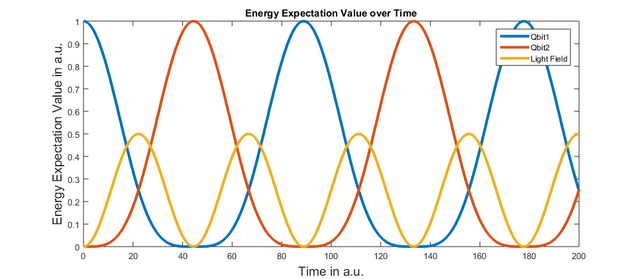
1 | plot(s.time,s.getEnergy('qbit1')); %plot the energy expectation value of the first qbit over time |
ergibt das folgende Diagramm (einige Beschriftungen ausgenommen):
Da alle Systeme in Resonanz sind, können wir volle Rabi-Zyklen sehen. Wenn ein System nicht in Resonanz wäre, wären die Amplituden viel kleiner. Probieren Sie es aus, indem Sie den Code kopieren und einfügen und dabei einen der Werte für die Energielücke ändern.