7. Kohärente Multidimensionale Spektroskopie - Die CMDS-Klasse - QDT

Die Simulation zweidimensionaler (2D) Spektren ist generell schwierig. Sie könnten versuchen, 2D-Spektren mithilfe der Toolbox manuell zu simulieren. In diesem Fall müssten Sie Schleifen über Simulationen schreiben, externe Feldverzögerungen und Phasen ändern, Phase Cycling durchführen und mehr. Um diese sich wiederholende Arbeit, die für alle mehrdimensionalen Spektroskopie-Experimente ähnlich ist, zu vereinfachen, haben wir die Klasse CMDS (Coherent Multidimensional Spectroscopy) aufgenommen. Diese Klasse nimmt einen anderen Platz in der Toolbox-Struktur ein, indem sie eine Instanz der System-Klasse nimmt und mehrere Simulationen mit unterschiedlichen Interpulsparametern innerhalb eines mehrpulsigen externen Lichtfelds durchführt. Um die CMDS-Klasse zu verwenden, müssen Sie auf die übliche Weise ein Systemobjekt definieren. In unserem einfachen Beispiel unten haben wir nur ein einzelnes Qbit, an dem wir ein populationsbasiertes 2D-Experiment durchführen, bei dem wir den Beitrag des Photonenechosignals durch eine Dreipulssequenz berechnen.

1
2
3
4
5
6
7
8
9
10
11
12
13

s = System;
s.lso = true;  %use the lindblad superoperator

gaps = [2.0*s.evtoau];
a = Nlevel(gaps);
a.setDipole([1 0], 1);
s.addEntity(a, 'molecule');
s.addDissipation('molecule', 50*s.fstoau, [1 0]);
s.addDecoherence('molecule', 30*s.fstoau, [1 0]);
s.setTmax(500*s.fstoau);
s.setTimestep(0.1*s.fstoau);

c = CMDS(s);

In diesem Beispiel verwenden wir, anders als in allen anderen Beispielen, Werte, die man auch in einem echten Experiment verwenden würde. Beachten Sie hierbei die Variablen fstoau und evtoau. Die System-Klasse hat viele solcher Felder für Umrechnungsfaktoren in und aus atomaren Einheiten.

Das zu simulierende System wird an den CMDS-Konstruktor übergeben. Im nächsten Schritt müssen wir mehrere Variablen angeben, die für die Durchführung der 2D-Spektroskopie erforderlich sind.

1
2
3
4
5
6
7
8
9
10
11

% Experimental parameters
gamma0 = 0.0; %0.0 = full rotating frame; 1.0 = lab frame
E0 = 2.0*s.evtoau; % Central energy of the laser pulses
amp=5e-4; %external field amplitude
t_pulse = 20*s.fstoau; %pulse duration (FWHM)
c.setdelayMaxs([100 120 120]*s.fstoau); %Three-pulse sequence, with the first pulse starting at 100 fs with delays scanned up to 120 fs
c.setdelaySteps([21 21]);
c.setPcScheme([1 5 2]); %Phase cycling scheme for photon echo contribution
c.setContributions([-1 2 -1]);
c.setEfieldparameter(amp,t_pulse,E0,gamma0);
c.setReturnFunction(returnExcited)

Im oberen Teil werden nur einige Parameter definiert, aber im unteren Teil wird es interessant. Gehen wir den Code Zeile für Zeile durch.

c.setdelayMaxs([100 120 120]*s.fstoau);

Dieser Befehl nimmt einen Vektor mit Zeitverzögerungen entgegen. Die Anzahl der angegebenen Zeitverzögerungen bestimmt die Anzahl der in der Simulation verwendeten Impulse. Hier geben wir drei Verzögerungen an. Der erste Wert bezeichnet immer den Abstand des ersten Impulses von t=0. Die nächsten beiden Werte bestimmen die maximalen Verzögerungen zwischen aufeinanderfolgenden Impulsen. Daher haben wir eine Dreipulssequenz definiert.

c.setdelaySteps([21 21]);

definiert die Anzahl der Schritte, mit denen jede Verzögerungzeit abgetastet wird. Da wir eine Dreipulssequenz haben, müssen wir zwei Schrittnummern angeben. Wenn der angegebene Vektor die falsche Länge hat, gibt CMDS einen Fehler aus.

c.setPcScheme([1 5 2]);
c.setContributions([-1 2 -1]);

Legt das Phase-Cycling-Schema der Pulszüge fest. Eine detaillierte Beschreibung der Auswahl eines geeigneten Phasenzyklusschemas finden Sie in Ref. [1]. Hier haben wir ein 1×5×2-Phase-Cycling-Schema gewählt, um nur den Photonenechobeitrag zu berechnen. Mit c.setContributions stellen wir die Gewichtungsparameter eines Standardsignalbeitrags (das Photonenecho) bereit, der benötigt wird, um anschließend das 2D-Spektrum aus dem Rohsimulationsdatensatz zu extrahieren.

c.setEfieldparameter(amp,t_pulse,E0,gamma0);

legt die externen Feldparameter fest, die sich im Verlauf mehrerer Simulationsdurchläufe nicht ändern.

Hinweis: QDT bietet eine Twopulse.m-, Threepulse.m- und Fourpulse.m-Funktion, wie sie für kohärente mehrdimensionale Spektroskopie verwendet werden können. Der Benutzer kann diese Funktionen jedoch nach Belieben wählen und an sein Experiment anpassen.

Bei der Simulation von 2D-Spektroskopie werden große Datenmengen erzeugt. Normalerweise sind für den Benutzer nur bestimmte Attribute der resultierenden Dichtematrizen von Interesse. Daher ermöglicht die CMDS-Klasse dem Benutzer, eine Rückgabefunktion bereitzustellen, was im Beispiel oben mit folgendem Befehl erfolgt:

c.setReturnFunction(returnExcited)

Die Ergebnisse dieser Rückgabefunktion werden in der Variable CMDSdata gespeichert. Die hier verwendete Beispiel-Rückgabefunktion lautet

1
2
3
4
5
6

function out = returnExcited
    out = @inner;
    function out2 = inner(s)
         out2 = sum(squeeze(s.rho_hist(2,2,:))); %note that matlab indexing starts at 1
    end
end

und gibt daher die zeitintegrierte Population des ersten angeregten Zustands, für jede abgeschlossene Simulation mit einem bestimmten Pulszug, zurück. Eine Rückgabefunktion muss einen Funktionszeiger zurückgeben, der ein System-Objekt als Parameter verwendet.

Führen wir nun die eigentliche Berechnung durch:

1 2	c.parallel = true % enable parallel computing c.generate_CMDS('molecule');

Die Variable parallel ermöglicht es Matlab, die Rechenlast auf mehrere CPUs zu verteilen. Wenn Sie keinen Zugriff auf einen Rechencluster haben, kann die Berechnung eine Weile dauern. Nach Abschluss der Simulation werden die Ergebnisse in CMDSdata gespeichert. Die CMDS-Klasse bietet eine Beispiel-Auswertungsfunktion plotCMDS. Für den vorliegenden Fall rufen wir diese Funktion auf mit

1
2
3

plotContribution = [-1 2 -1]; %weighting factors
nzp = 5; %5-fold zero padding
c.plotCMDS(plotContribution,1,1,nzp,'rephasing');

plotCMDS akzeptiert viele Parameter. Eine detaillierte Beschreibung finden Sie in der Begleitdokumentation von plotCMDS. Der obige Code erzeugt die folgende Ausgabe:

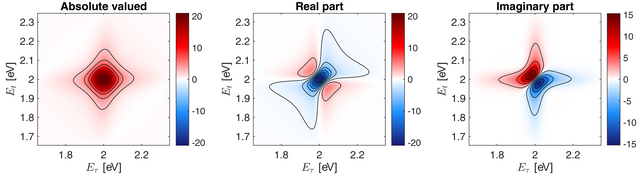
Hier wird das absolutwertige Photonenechospektrum zusammen mit seinem Real- und Imaginärteil angezeigt. Eine Resonanz tritt bei genau (2.0, 2.0) eV auf, was identisch mit der Systemresonanz ist, die wir oben definiert haben.

Hinweis: plotCMDS stellt nur ein Beispiel-Plottool dar, mit dem Sie schnell Feedback zu einem Simulationsergebnis erhalten können, und daher fehlen in seiner aktuellen Implementierung möglicherweise erweiterte Datenanalysefunktionen. Natürlich können Sie Ihre eigenen angepassten Auswertungs- und Plottools verwenden. Zu diesem Zweck kann die Rohsimulationsausgabe (Rohdatenmatrix und Zeitachsen in Femtosekunden), die Sie mit Ihrem eigenen Skript verarbeiten möchten, im Workspace gespeichert werden, indem Sie Folgendes aufrufen:

1
2
3

resultCMDSdata = c.CMDSdata;
tau_delay = c.delayAxes{1}/s.fstoau;
t_delay = c.delayAxes{2}/s.fstoau;

Die CMDS-Klasse ist für die Simulation populationsbasierter 2D-Spektroskopie optimiert und unterstützt in ihrem aktuellen Zustand die Simulation von Zwei-, Drei- und Vierpulsexperimenten.

Literaturverzeichnis

[1] H.-S. Tan, Theory and phase-cycling scheme selection principles of collinear phase coherent multidimensional optical spectroscopy, J. Chem. Phys. 129, 124501 (2008).

Bildnachweise