2. Dissipation, Dephasierung und Laserpulse - QDT

Um den Realismus unserer Simulation zu erhöhen, fehlen uns zwei Hauptbestandteile, die in fast jedem Versuchsaufbau vorhanden sind. Externe Laserpulse, die das System anregen, und die Dissipation und Dephasierung, die ein Quantensystem erfährt, wenn es mit der Umgebung interagiert.

Dissipation und Dephasierung werden über den Lindblad-Formalismus implementiert (für detailliertere Informationen schauen Sie bitte in die Dokumentation der Funktion addDissipation oder in das technische Paper). Um qbit1 einen dissipativen Kanal hinzuzufügen, fügen wir dem obigen Quellcode die folgende Codezeile hinzu (an einer beliebigen Stelle, nachdem qbit1 definiert wurde und bevor der Simulationsbefehl aufgerufen wird):

s.addDissipation('qbit1',50);

Dies ergibt die folgende Abbildung:

Als Parameter verwendet die Funktion addDissipation den Namen des Subsystems, das Energie an die Umgebung verliert, sowie die Lebensdauer der Population im angeregten Zustand. Folglich zerfällt die Population im angeregten Zustand von qbit1 nach 50 a.u. auf 1/e-tel ihres ursprünglichen Wertes. Beachten Sie, dass die Population nur dann zerfällt, wenn in qbit1 tatsächlich eine Population vorhanden ist. Wir haben den Gesamtenergieerwartungswert des Systems zum Diagramm hinzugefügt. Wie Sie sehen, nimmt er nur ab, wenn in qbit1 Energie (und damit eine Population im angeregten Zustand) vorhanden ist.

Der Dephasierungsbefehl funktioniert analog und ermöglicht dem Benutzer die Implementierung eines reinen Dephasierungsprozesses, der zu einem Verlust von Phaseninformationen innerhalb des Systems, aber zu keinem Energieverlust führt.

Beliebige externe Felder können über den Befehl addExternalField hinzugefügt werden, der zwei Parameter verwendet: eine externe Feldfunktion und das Subsystem, mit dem das externe Feld interagiert. Sehen wir uns an, wie dies in der Praxis aussieht:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

clear; close all;
s = System; %create a System
s.addEntity(Nlevel(1),'qbit1'); %add the created qbit and call it qbit1
s.addEntity(Qoscillator(3,1),'cavity'); %add a quantum harmonic oscillator with 5 levels and energydiffernce of 1 a.u.
s.addEntity(Nlevel(1),'qbit2'); %add another qbit and call it qbit2
s.addCoupling('qbit1','cavity',0.05); %add a coupling between the first qbit and the cavity
s.addCoupling('qbit2','cavity',0.05); %add a coupling between the second qbit and the cavity
s.addDissipation('qbit1',50); %Set the lifetime of qbit1 to 50 a.u.
s.addExternalField(Gausspulse(0.04,50,30,1),'qbit1'); %set an external electric field that interacts only with qbit1
%done

s.setTmax(200); %set the maximum time
s.setTimestep(0.1);
s.simulate; % start the simulation

Das sieht sehr kompliziert aus. Was ist Gausspulse und warum hat er so viele Parameter? Keine Sorge, Gausspulse ist eigentlich etwas, das Sie selbst definieren können. Hier ist die Matlab-Funktion, die auch eine Vorlage ist, die Sie für jede Feldfunktion verwenden können, die Sie definieren möchten:

1
2
3
4
5
6
7

function [ out ] = Gausspulse(amp,td,tp,we) %td = delay time, tp = pulse width, we = frequency
%Gaussian pulse (external electric field)
out = @inner;
function exF = inner(t)
exF = amp*exp(-2*log(2)*((t-td)/(tp)).^2) .* cos(we*(t-td)); %external field
end
end

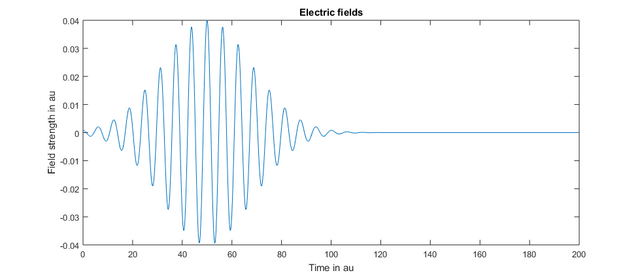
Die äußere Funktion gibt einen Zeiger auf die innere Funktion zurück (die entsprechend benannt ist). Die Idee dahinter ist, dass die innere Funktion, die an das System-Objekt übergeben wird, immer einen einzigen Parameter benötigt, nämlich den Zeitvektor. Der Zeitvektor wird dann später von der System-Klasse bereitgestellt. Die Struktur wird auf diese Weise aufgebaut, da das System-Objekt keine Kenntnis von anderen Variablen Ihrer Laserpulsfunktion wie der Pulsbreite haben kann. Daher übernimmt die äußere Funktion alle diese anderen Parameter. Im Fall von Gausspulse sind dies: Amplitude, Zeitverzögerung, Pulsbreite und Frequenz. So sieht der oben definierte Laserpuls aus:

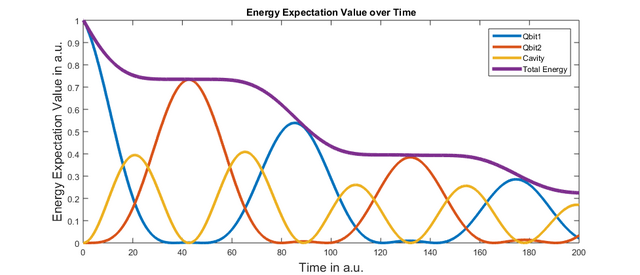
Sie können dieses Diagramm ganz einfach mit der Funktion plotEfields der System-Klasse erstellen. Wenn wir die letzte Iteration unserer Simulation ausführen und die Energiewerte darstellen, erhalten wir:

Beachten Sie, dass wir die Zeile entfernt haben, in der wir qbit1 zu Beginn der Simulation in einen angeregten Zustand versetzt haben, und außerdem eine Zeile für einen dissipativen Kanal von qibt1 hinzugefügt haben. Wie Sie sehen, beginnt das System mit allen Entitäten im Grundzustand und es zunächst passiert absolut nichts. Wenn der Laserpuls auf das System einwirkt, wird Energie in qbit1 und anschließend in die Kavität und qbit2 übertragen. Interessanterweise wird die höchste Amplitude des Energieerwartungswerts und damit der Besetzung zu jedem Zeitpunkt von qbit2 gehalten, das nicht direkt mit dem externen Feld interagiert.

Bildnachweise