4. Polarisation, Fourier-Analyse und Suszeptibilität

Eine weitere interessante Variable ist die Polarisation eines Subsystems, da diese oft über ein Experiment zugänglich ist. QDT bietet eine Funktion getPolarisation(name), die die Polarisation eines bestimmten Subsystems über den Zeitverlauf zurückgibt. Der Polarisationsoperator hängt von den unterschiedlichen Dipolmomenten zwischen den Energieniveaus ab, die mit der Methode setDipole festgelegt werden können. Die Methode getPolarisation berücksichtigt diese Dipolmomente.

1 2 3 4 5 6 7 8 9 10 11 12 13 14

s = System; %create a System s.addEntity(Nlevel(1),'qbit1'); %add the created qbit and call it qbit1 s.addEntity(Qoscillator(3,1),'cavity'); %add a quantum harmonic oscillator with 5 levels and energydiffernce of 1 a.u. s.addCoupling('qbit1','cavity',0.05); %add a coupling between the first qbit and the cavity s.addDissipation('qbit1',50); %Set the lifetime of qbit1 to 50 a.u. s.addDissipation('cavity',50); %Set the lifetime of the cavity to 50 a.u. s.addExternalField(Gausspulse(0.04,50,30,1),'qbit1'); %set an external electric field that interacts only with qbit1 %done s.setTmax(400); %set the maximum time s.setTimestep(0.1); s.simulate; % start the simulation h = plot(s.time,s.getPolarisation('qbit1'));

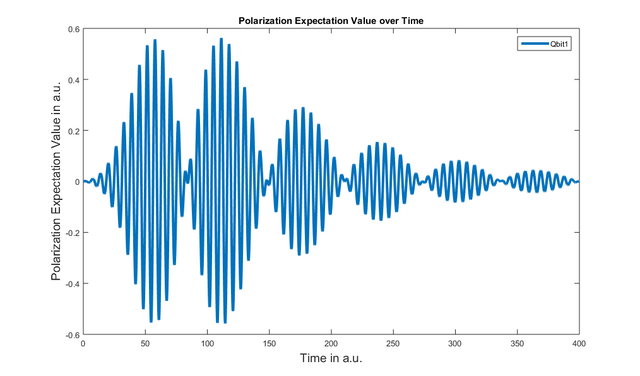
Das obige Beispiel stellt die Polarisation eines Qbits in einer Kavität dar und ergibt die folgende Abbildung:

Allerdings ist es ziemlich schwierig, diese Daten zu interpretieren. Um mehr Informationen daraus zu gewinnen, müssen wir eine Fourier-Analyse durchführen.

Die Standardimplementierung der FFT (Fast Fourier Transformation) gibt ein gespiegeltes Spektrum zurück und liefert nicht den zugehörigen Frequenzvektor, was fehleranfällig ist. Aus diesem Grund bietet die Systemklasse ihre eigene fft-Funktion und liefert den passenden Frequenzvektor. Darüber hinaus wird die Methode setdf bereitgestellt. Wenn diese Methode aufgerufen wird, wird der Frequenzvektor mit dem neuen Frequenzinkrement neu konstruiert. Darüber hinaus werden alle zukünftigen Aufrufe der fft-Methode des System-objekts den Eingabedaten Nullen hinzufügen, um die erforderliche Signallänge zu erreichen. Die Ausführung von

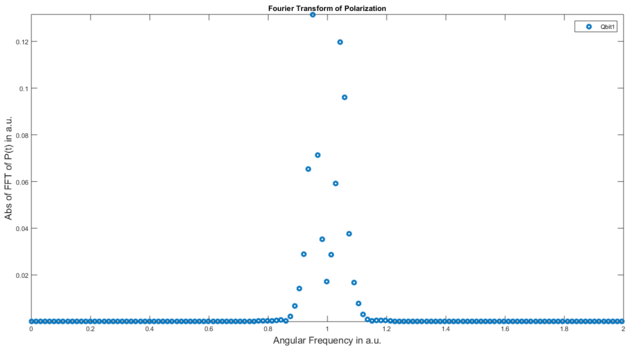
plot(2*pi*s.f, abs(s.fft(s.getPolarisation(‘qbit1′))),’o’); axis([0 2 -inf inf]);

ergibt:

was nicht schlecht ist, aber die Auflösung ist für unseren Geschmack etwas zu niedrig. Beachten Sie die Parameter des obigen Plot-Befehls. "s.f" enthält den Frequenzvektor, der von der System-Klasse verwaltet wird. "s.fft" führt eine Fourier-Transformation des bereitgestellten Vektors durch (dieser Vektor muss dieselbe Länge wie der Zeitvektor der System-Klasse haben, alle System-Funktionen wie getEnergy geben einen solchen Vektor zurück). Da der resultierende Vektor komplex ist, nehmen wir den Absolutwert seiner Einträge mithilfe der "abs"-Funktion von Matlab.

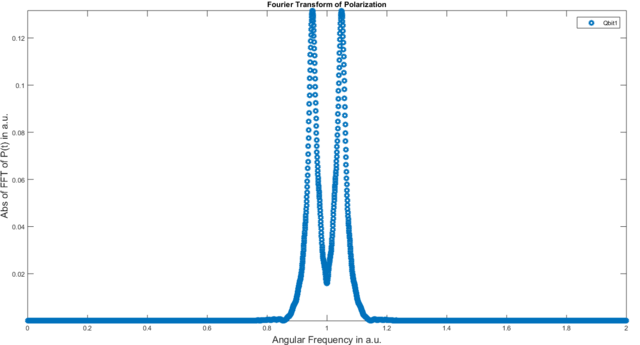
Um die Auflösung unseres Fourier-transformierten Signals zu erhöhen, können wir die setdf-Funktion verwenden. Der Aufruf von

s.setdf(0.0001); h =plot(2*pi*s.f, abs(s.fft(s.getPolarisation(‘qbit1′))),’o’); axis([0 2 -inf inf]);

führt zu:

Wir können nun deutlich die beiden relevanten Peaks sehen, die um die Resonanzfrequenz zentriert sind. Es gibt zwei Peaks statt einem, da Qbit und Kavität miteinander gekoppelt sind und somit analog zu zwei klassischen Pendeln eine Mode mit höherer und eine mit niedrigerer Resonanzfrequenz erzeugen. Je nach Kopplungsstärke ist dieser Effekt stärker oder schwächer.

 

Suszeptibilität

Die Suszeptibilität kann als Maß für die Systemreaktion betrachtet werden, normalisiert durch das angelegte externe Feld. Um sie zu berechnen, stellt QDT die Funktion getSusceptibility zur Verfügung. Weitere Informationen finden Sie in der Matlab-Dokumentation.