3. Spezifische Kopplung, Dissipation und Dipole
Bis zu diesem Punkt haben wir mit Qbits gearbeitet und für einen Qbit reichen die bisher vorgestellten Mechanismen für Kopplung, Dissipation und externe Laserpulse aus. Nehmen wir jedoch an, wir haben ein System, das aus zwei Subsystemen A und B mit je drei Energieniveaus besteht. Nun kann der Übergang zwischen den Zuständen |0> und |1> von Subsystem A mit einer anderen Stärke an den |0> – |1> Übergang von Subsystem B koppeln als beispielsweise der |0> – |2> Übergang von A an den |1> – |2> Übergang von B. Mit anderen Worten, wir brauchen eine Möglichkeit, die Kopplung zwischen beliebigen Übergängen einzustellen und zu aktivieren und zu deaktivieren. Dazu ist kein zusätzlicher Befehl erforderlich. Vielmehr ist die Methode addCoupling stark überladen. Sehen Sie sich den folgenden Code an:
1 | s = System; %create a System |
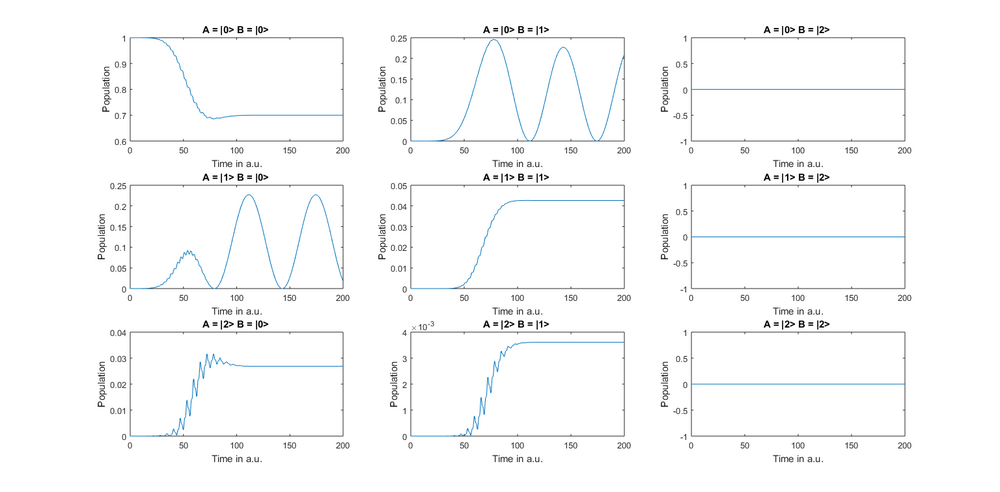
Dies implementiert ein System, in dem nur die |0> – |1> Übergänge von A und B miteinander koppeln. Wir können uns die resultierenden Diagonalelemente der Dichtematrix mit dem Befehl plotoccupation der System-Klasse ansehen (der Befehl plotoccupation stellt immer alle Diagonalelemente der Dichtematrix über die Zeit dar, wenn Sie keinen Parameter angeben).
Wie Sie sehen, verschiebt der Laser eine beträchtliche Population in den Zustand A= |2> B = |0>. Diese Population nimmt jedoch nie ab, da es keinen Kopplungsterm gibt, der sie mit dem Zustand A = |0> B = |2> koppelt. Das "[1 0]" hinter dem "A" im addCoupling-Befehl definiert, dass diese Kopplung nur für den Übergang |0> – |1> im Subsystem A gilt. Dasselbe gilt für den Term "[1 0]" hinter "B". Wenn wir einen solchen Term weglassen, wird die Kopplung für alle Übergänge eines Subsystems implementiert. Wenn also das "[1 0]" hinter "B" fehlen würde, würde der Übergang |0> – |1> von A mit allen Übergängen des Subsystems B gekoppelt. Und wenn beide "[1 0]" fehlen würden, würden alle Übergänge von A mit allen Übergängen von B gekoppelt. Wenn Sie also unterschiedliche Kopplungsstärken zwischen verschiedenen Übergängen wünschen, können Sie mehrere spezifische addCoupling-Befehle verwenden. Beachten Sie, dass addCoupling dem System einen Dipol-Dipol-Hamiltonoperator hinzufügt, der von Natur aus resonanzabhängig ist. Selbst wenn also ein Übergang der E = 1 a.u. eine starke Kopplungsstärke zu einem Übergang von E = 1.5 a.u. hat, wird fast keine Energie übertragen (es sei denn, Sie haben aufgrund von Dissipation und Dephasierung eine sehr große Linienbreite).
Dasselbe Prinzip gilt für Dissipations- und Dephasierungsterme. Die Population zerfällt mit unterschiedlichen Raten zwischen |1> – |0>, |2> – |0> und |2> – |1>. Um der Simulation eine bestimmte Dissipation zwischen |1> und |0> von Subsystem A hinzuzufügen, verwenden Sie:
s.addDissipation(‘A’, 50, [1 0]); |
Auch hier gilt: Wenn der dritte Parameter nicht angegeben wird, fügt addDissipation einen Dissipationseffekt zwischen allen möglichen Übergängen hinzu.
Die Toolbox ist so aufgebaut, dass Sie sie auch verwenden können, wenn Sie gerade erst anfangen und sich noch keine Gedanken über fortgeschrittene Themen gemacht haben. Wenn Sie nach ein bisschen Herumprobieren feststellen „Mir fehlt mir noch dies und das …“, können Sie es normalerweise ganz einfach hinzufügen, indem Sie denselben Befehlen, die Sie zuvor verwendet haben, zusätzliche Parameter zuweisen.
Zuletzt haben wir externe Laserpulse. Diese interagieren mit einem Übergang in einem Subsystem entsprechend dem Dipolmoment dieses Übergangs. Folglich benötigen wir eine Möglichkeit, Dipolmomente einzustellen. (Derzeit unterstützt die Toolbox nur skalare Dipolmomente und skalare elektrische Felder. Wenn Sie ein Molekül haben, in dem unterschiedliche Dipolmomente in unterschiedlichen Winkeln zum eingehenden Feld stehen, müssen Sie dies durch Einstellen der Dipolstärke erfassen.) Die Klasse Nlevel verfügt über die erforderliche Methode, die passenderweise setDipole heißt. Um die Methode setDipole zu verwenden, muss das Nlevel-Objekt separat definiert und später dem Gesamtsystem hinzugefügt werden:
1 | a = Nlevel([1 1]); |
Als ersten Parameter verwendet setDipole die Level, zwischen denen das Dipolmoment eingestellt wird. Der zweite Parameter ist das Dipolmoment. Standardmäßig sind alle Dipolmomente auf eins eingestellt (wiederum in atomaren Einheiten).
Hinweis: Wenn der Befehl setDipole einmal aufgerufen wird, werden alle anderen Dipolmomente des Subsystems auf null gesetzt! Wenn ein Dipolmoment manuell definiert wird, müssen alle Dipolmomente vom Benutzer bereitgestellt werden.
Das separate Definieren eines Subsystems hat den zusätzlichen Vorteil, dass der Benutzer mithilfe der Standard-Matlab-Schnittstelle alle Variablen des erstellten Objekts, beispielsweise die Dipolmatrix, anzeigen kann.