5. Verschränkung, partielle Spuren und Bloch-Vektoren - QDT

Dieses Kapitel befasst sich mit einigen fortgeschrittenen Funktionen, die im Zusammenhang mit Quanten-Computing nützlich sind. Die Verschränkung zwischen zwei Qbits ist für Quantencomputeroperationen von entscheidender Bedeutung, jedoch überraschend schlecht definiert. Es gibt mehrere Messmethoden für die Verschränkung. Eine sehr beliebtes Prinzip ist die sogenannte Gleichzeitigkeit. Leider ist diese Messung nur für reine Zustände gültig (Zustände, die keinen Dekohärenzprozess durchlaufen haben). Für beliebige Zustände mit zwei Qbits ist das Wootters-Maß für die Verschränkung besser geeignet (siehe [1]). Es ist recht komplex zu berechnen, aber glücklicherweise bietet die Toolbox eine Methode getEntanglement(name1,name2), die die Wootters-Verschränkung zwischen den beiden Qbits mit name1 und name2 zurückgibt. SIehe folgendes Beispiel:

1
2
3
4
5
6
7
8
9
10
11
12
13

s = System; %create a System
s.addEntity(Nlevel(1),'qbit1'); %add a qbit and call it qbit1
s.addEntity(Nlevel(1),'qbit2'); %add another qbit and call it qbit2
s.addCoupling('qbit1','qbit2',0.05); %add a coupling between the qbits
s.addDissipation('qbit1',500); %Set the lifetime of qbit1 to 500 a.u.
s.addDissipation('qbit2',500); %Set the lifetime of qbit2 to 500 a.u.
s.addExternalField(Gausspulse(0.04,50,30,1),'qbit1'); %set an external electric field that interacts only with qbit1

s.setTmax(400); %set the maximum time
s.setTimestep(0.1);
s.simulate; % start the simulation

plot(s.time,s.getEntanglement); % plot the Entanglement

Mittlerweile sollte Ihnen der Code ziemlich vertraut vorkommen. Wir haben ein System aus zwei gekoppelten Qbits. getEntanglement benötigt keine Parameter, da es nur mit einer Dichtematrix aus zwei Qbits arbeiten kann. Das resultierende Diagramm sieht folgendermaßen aus:

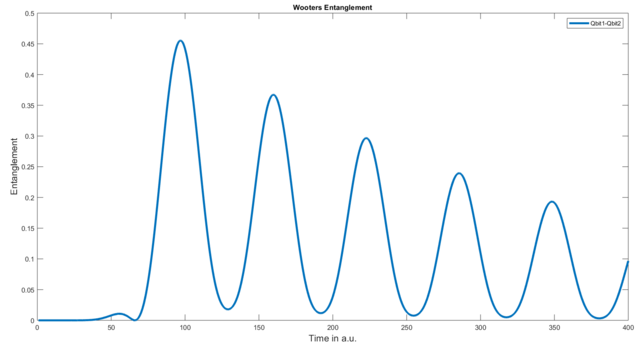
Nehmen wir nun aber an, wir haben mehr als zwei Qbits in unserer Simulation, wie im Beispiel mit der Kavität. Die Verschränkung zwischen ihnen hat immer noch eine physikalische Bedeutung, aber die Dichtematrix ist viel größer und wir können die Verschränkung nicht direkt extrahieren.

Hier kommen partielle Spuren ins Spiel. Partielle Spuren (die (fast) nichts mit der typischen Spur einer Matrix gemeinsam haben) ermöglichen es uns, ein bestimmtes Subsystem „herauszufiltern“. Die resultierende Dichtematrix hat kleinere Dimensionen und beschreibt alle Subsysteme, über die nicht die Spur gebildet wurden. Dies kann im Allgemeinen für viele Anwendungen nützlich sein. In diesem Tutorial werden wir es nur für die Verschränkung verwenden. Die Methode traceOut(name) der Systemklasse muss nach einer abgeschlossenen Simulation aufgerufen werden. Die reduzierten Dichtematrizen sind in einem anderen dreidimensionalen Array namens "reduced_rho_hist" verfügbar. Mehrere Subsysteme können nacheinander verfolgt werden. Die Methode getEntanglement funktioniert mit den reduzierten Dichtematrizen, wenn sie die richtige Dimensionalität haben, und gibt andernfalls einen Fehler aus. Sehen Sie sich dieses Beispiel an:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

s = System; %create a System
s.addEntity(Nlevel(1),'qbit1');
s.addEntity(Nlevel(1),'qbit2');
s.addEntity(Qoscillator(3,1),'cavity');
s.addCoupling('qbit1','cavity',0.05);
s.addCoupling('qbit2','cavity',0.05);
s.addDissipation('qbit1',500);
s.addDissipation('qbit2',500);
s.addDissipation('cavity',400);
s.addExternalField(Gausspulse(0.04,50,30,1),'qbit1');

s.setTmax(400); %set the maximum time
s.setTimestep(0.1);
s.simulate; % start the simulation

s.traceOut('cavity');
h = plot(s.time,s.getEntanglement);

Der Code oben liefert das folgende Diagramm:

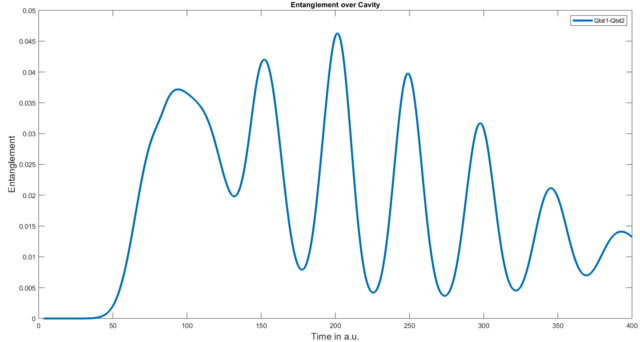
Als nächsten Schritt könnten dieser Abbildung beispielsweise Energie- oder Populationsdiagramme hinzufügen und sehen, wie sich die Verschränkung in Bezug darauf verhält.

Bloch-Vektoren sind ein Werkzeug, um den Zustand eines Qbits genauer zu untersuchen. Die System-Klasse bietet die Methoden blochsphere(name) und animateBlochsphere(name). Um mehr über ihre Funktion zu erfahren, werfen Sie bitte einen Blick in die Matlab-Dokumentation.

Literaturverzeichnis

[1] W. K. Wootters, Entanglement of formation of an arbitrary state of two qubits, Phys. Rev. Lett. 80, 2245 (1998).

Bildnachweise